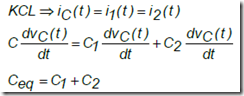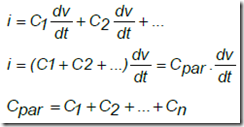As the relationship on a series of resistors, capacitors can also be connected in parallel, series, or a combination of series and parallel. In parallel relationship, Figure 1.91. shows two capacitors connected in parallel, or both capacitors connected in parallel can be represented by a single capacitor as a replacement element. As the nature of the parallel relationship, that, overall, both the capacitor charging voltage gets an equal and with the same time anyway.
Thus the amount of the total charge QT on a parallel circuit can be determined as the following equation:
QT = Q1 + Q2
because the connection charge is Q = C V, then each capacitor can be charged by:
Q1 = C1. V; Q2 = C2.V; QT = CT.V
therefore:
CT.V = C1. V + C2.V
then the magnitude of the total capacitance in parallel circuit is
CT = C1. + C2 + ……… ..Cn
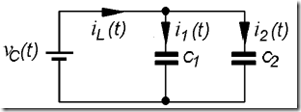
Figure 5.10. The series of two capacitors mounted in parallel
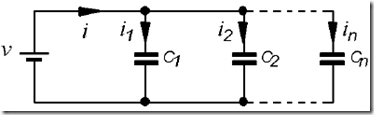
Figure 5.11. N circuit capacitor mounted in parallel
Based on the above equation, then the value of the total capacitance is equal to the sum total of each capacitor. Thereby connecting the capacitors in parallel in principle is the same as enlarging cross-sectional area (A = A1 + A2) from the condenser to the condenser-series connection in principle the same as the parallel relationship, Figure 1.94. shows two capacitors connected in series, or a second capacitor connected so it can also be represented by a single capacitor as a replacement element.
As the nature of the series connection, that the magnitude of the voltage divider charging overall in each of the capacitors is: VT = V1 + V2 Due to the series connection in seiap capacitor has a charging voltage is different, thus the amount of charge on each capacitor is the same ( QT = Q1 = Q2 = Q). From the above equations obtained relationship voltage V = Q / C, thus the magnitude of the voltage on each capacitor is;
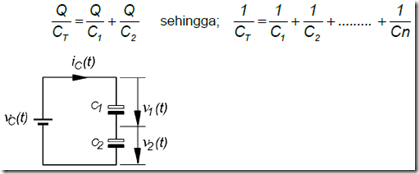
Figure 5.12. The series of two capacitors installed in series
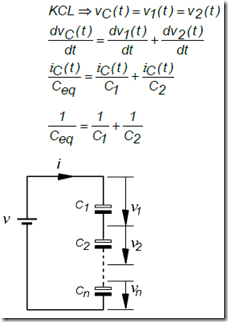
Figure 5.13. N The series capacitors installed in series
Working voltage capacitors (Working Voltage) is the maximum voltage that is allowed to work on a capacitor. Capacity expressed in units of Farad capacitor and the working voltage is expressed with the Volt. The working voltage condenser / Capacitors AC for non-polar: 25 Volt; 50 Volt; 100 Volt; 250 Volt to 500 Volt DC working voltage for polar: 10 Volt; 16 Volt; 25 Volt; 35 Volt; 50 Volt; 100 Volt; 250 Volt